初中数学初二上册《全等三角形》利用“转移法”构造全等三角形
为了能找到解决问题的办法,有时需要在图形中添加一些线,称为辅助线。辅助线的添加有利于使题目中的条件集中,能较容易找到一些量之间的关系,使问题得以解决。
例题1
如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为点D。
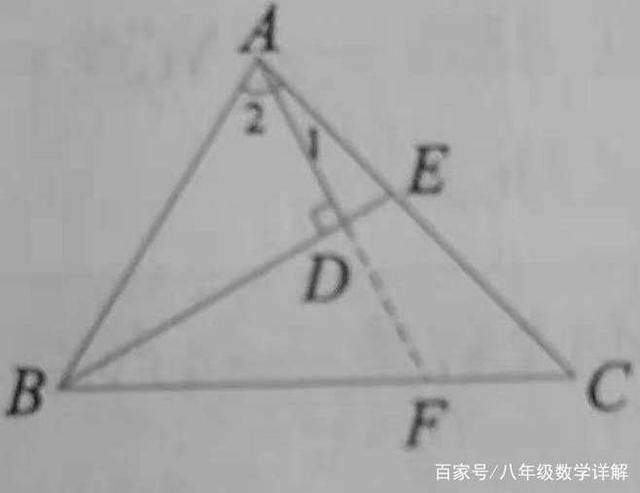
求证:∠2=∠1+∠C
1、从图形上看∠2和∠1、∠C没有什么直接的关系,本题的结论看似很难证明。但是我们只要把AD延长交BC于点F的话,那么∠DFB就和∠1、∠C有特殊的等量关系了,∠DFB=∠1+∠C(三角形的一个外角等于和它不相邻的两个外角的和)
2、现在我们的问题转换为证明∠2=∠DFB。观察图形我们可以发现∠DFB、∠2是△FBD和△ABD的对应角,只要证明△FBD和△ABD就行了。
3、由BE是∠ABC的平分线可以得到结论:∠ABD=∠FBD。由AD⊥BE可以得到结论:∠BDA=∠BDF=90°。再加上公共边BD就能够证明△ABD≌△FBD。
证明:
延长AD交BC于点F
∵BE是∠ABC的平分线
∴∠ABD=∠FBD
∵AD⊥BE
∴∠BDA=∠BDF=90°
在△ABD和△FBD中
∠ABD=∠FBD (已证)
BD=BD (公共边)
∠BDA=∠BDF (已证)
∴△ABD≌△FBD(ASA)
∴∠2=∠DFB(全等三角形的对应边相等)
∵∠DFB=∠1+∠C(三角形的一个外角等于和它不相邻的两个外角的和)
∴∠2=∠1+∠C
小结:在此题的证明过程中,主要采用了“把线、角进行转移”的方法。如果您认为我的分析对您有些帮助,请把文章分享给您的同学和朋友们。
声明:以上内容来自网络,若有侵权,请联系我们,立即删除!所有的观点由网友个人想法,不代表本公司也持此立场,感谢大家支持!
YMU教育(www.91ymu.com),全国热线电话:023-89119533;提供医学继续教育学分卡、中小学课后辅导服务、执业医师护士药师资格考试考前辅导等咨询服务;

